THUẬT TOÁN ĐIỀU KHIỂN CHÍNH XÁC PID

Bộ điều khiển PID là một bộ điều khiển vòng kín được sử dụng rộng rãi trong hệ thống điện, hệ thống tự động, điện tử. Mục tiêu của bộ điều khiển PID là điều chỉnh giá trị điều khiển ở ngõ ra Ouput sao cho sai lệch Error e(t) = (SP – PV) giữa giá trị đo được của hệ thống PV (Process Variable) với giá trị cài đặt SP (SetPoint) nhỏ nhất có thể (~ 0), đạt được sự ổn định và có đáp ứng nhanh.

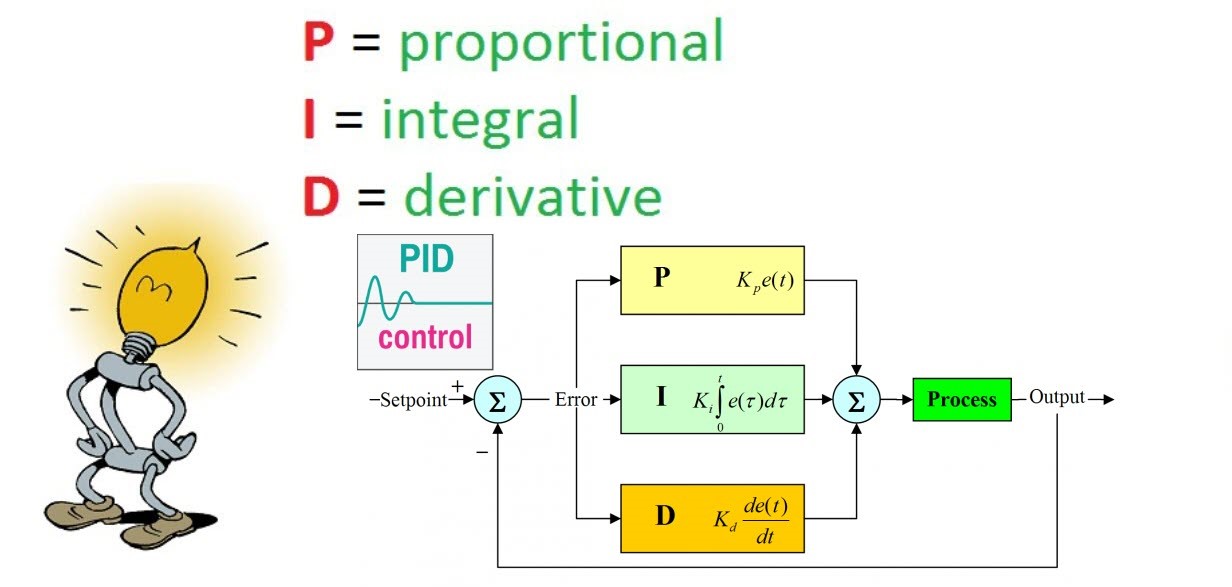
Thuật toán điều khiển chính xác PID (Hình minh họa)

PID được tạo thành từ cụm từ tiếng Anh đầy đủ là Proportional Integral Derivative. Đây là một cơ chế phản hồi vòng điều khiển trong các hệ thống điều khiển công nghiệp mà hiện nay được sử dụng rất rộng rãi. Bộ điều khiển này được đưa vào sử dụng nhiều nhất trong các hệ thống điều khiển vòng kín hay các hệ thống có tín hiệu phản hồi.

Bộ điều khiển PID sẽ giúp các máy công nghệ tính toán ra các giá trị sai số là hiệu số giữa các giá trị đo thông số về biển đối và giá trị đặt theo mong muốn của người thiết kế, người dùng. Thông qua các điều chỉnh giá trị điều khiển đầu mà mà nhờ đó hệ thống điều khiển khi thực hiện sẽ giảm được tối đa những sai số, cho hoạt động chính xác hơn và đạt hiệu quả cao hơn.

Để đạt những kết quả tốt nhất, các thông số của PID cần được sử dụng điều chỉnh theo tính chất của hệ thống nó được gắn vào. Trong trường hợp điều khiển giống nhau, cần tính toán đẻ các đặc thù của hệ thống để các thông số của PID được chuẩn xác và hiệu quả cao nhất khi làm việc.

Phân tích các thành phần của bộ điều khiển PID

PID là cách viết tắc của các từ Propotional (tỉ lệ), Integral (tích phân) và Derivative (đạo hàm). Tuy xuất hiện rất lâu nhưng đến nay PID vẫn là giải thuật điều khiển được dùng nhiều nhất trong các ứng dụng điều khiển tự động. Để giúp bạn có cái hiểu rõ hơn bản chất của giải thuật PID tôi sẽ dùng một ví dụ điều khiển vị trí của một car (xe) trên đường thẳng. Giả sử bạn có một xe (đồ chơi…) có gắn một động cơ DC. Động cơ sinh ra một lực để đẩy xe chạy tới hoặc lui trên một đường thẳng như trong hình.

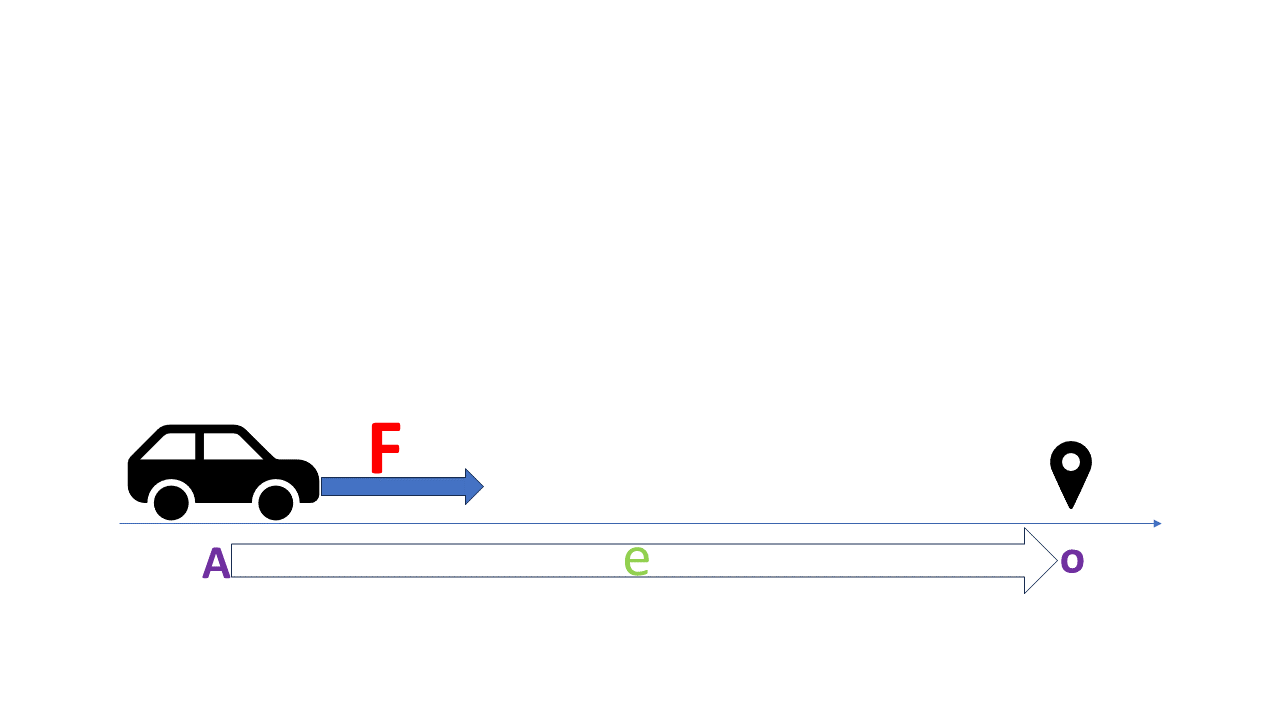
Một ví dụ thực tế về PID

Gọi F là lực do động cơ tạo ra điều khiển xe. Ban đầu xe ở vị trí A, nhiệm vụ đặt ra là điều khiển lực F (một cách tự động) để đẩy xe đến đúng vị trí O với các yêu cầu: chính xác (accurate),nhanh (fastresponse),ổn định (small overshot).

Một điều rất tự nhiên, nếu vị trí hiện tại của xe rất xa vị trí mong muốn (điểm O), hay nói cách khác sai số(error) lớn, chúng ta cần tác động lực F lớn để nhanh chóng đưa xe về O. Một cách đơn giản để công thức hóa ý tưởng này là dùng quan hệ tuyến tính:

F=Kp*e     (1)
Trong đó Kp là một hằng số dương nào đó mà chúng ta gọi là hệ số P (Propotional gain), e là sai số cần điều khiển tức khoảng cách từ điểm O đến vị trí hiện tại của xe. Mục tiêu điều khiển là đưa e tiến về 0 càng nhanh càng tốt. Rõ ràng nếu Kp lớn thì F cũng sẽ lớn và xe rất nhanh chóng tiến về vị trí O. Tuy nhiên, lực F quá lớn sẽ gia tốc cho xe rất nhanh (định luật II của Newton: F=ma). Khi xe đã đến vị trí O (tức e=0), thì tuy lực F=0 (vì F=Kp*e =Kp*0 =0) nhưng do quán tính xe vẫn tiếp tục tiến về bên phải và lệch điểm O về bên phải, sai số e lại trở nên khác 0, giá trị sai số lúc này được gọi là overshot (vượt quá). Lúc này, sai số e là số âm, lực F lại xuất hiện nhưng với chiều ngược lại để kéo xe về lại điểm O. Nhưng một lần nữa, do Kp lớn nên giá trị lực F cũng lớn và có thể kéo xe lệch về bên trái điểm O. Quá trình cứ tiếp diễn, xe cứ mãi dao động quanh điểm O. Có trường hơp xe dao động càng ngày xàng xa điểm O. Bộ điều khiển lúc này được nói là không ổn định. Một đề xuất nhằm giảm overshot của xe là sử dụng một thành phần “thắng” trong bộ điều khiển. Sẽ rất lý tưởng nếu khi xe đang ở xa điểm O, bộ điều khiển sinh ra lực F lớn nhưng khi xe đã tiến gần đến điểm O thì thành phần “thắng” sẽ giảm tốc độ xe lại. Chúng ta điều biết khi một vật dao động quanh 1 điểm thì vật đó có vận tốc cao nhất ở tâm dao động (điểm O). Nói một cách khác, ở gần điểm O sai số e của xe thay đổi nhanh nhất (cần phân biệt: e thay đổi nhanh nhất  không phải e lớn nhất). Mặt khác, tốc độ thay đổi của e có thể tính bằng đạo hàm của biến này theo thời gian. Như vậy, khi  xe từ A tiến về gần O, đạo hàm của sai số e tăng giá trị nhưng ngược chiều của lực F (vì e đang giảm nhanh dần). Nếu sử dụng đạo hàm làm thành phần “thắng” thì có thể giảm được overshot của xe. Thành phần “thắng” này chính là thành phần D (Derivative) trong bộ điều khiển PID mà chúng ta đang khảo sát. Thêm thành phần D này vào bộ điều khiển P hiện tại, chúng ta thu được bộ điều khiển PD như sau:

F=Kp*e+Kd*(de/dt)   (2)

Trong đó (de/dt) là vận tốc của sai số e và Kd là một hằng số không âm gọi là hệ số D (Derivative gain).

Sự hiện diện của thành phần D làm giảm overshot của xe, khi xe tiến gần về O, lực F gồm 2 thành phần Kp*e > =0 (P) và Kd*(de/dt) <=0 (D). Trong một số trường hợp thành phần D có giá trị lớn hơn thành phần P và lực F đổi chiều, “thắng” xe lại, vận tốc của xe vì thế giảm mạnh ở gần điểm O. Một vấn đề nảy sinh là nếu thành phần D quá lớn so với thành phần P hoặc bản thân thành phần P nhỏ thì khi xe tiến gần điểm O (chưa thật sự đến O), xe có thể dừng hẳn, thành phần D bằng 0 (vì sai số e không thay đổi nữa), lực F = Kp*e. Trong khi Kp và e lúc này đều nhỏ nên lực F cũng nhỏ và có thể không thắng được lực ma sát tĩnh. Bạn hãy tưởng tượng tình huống bạn dùng sức của mình để đẩy một xe tải nặng vài chục tấn, tuy lực đẩy tồn tại nhưng xe không thể di chuyển. Như thế, xe sẽ đứng yên mãi dù sai số e vẫn chưa bằng 0. Sai số e trong tình huống này gọi là steady state error (tạm dịch là sai số trạng thái tĩnh). Để tránh steady state error, người ta thêm vào bộ điều khiển một thành phần có chức năng “cộng dồn” sai số. Khi steady state error xảy ra, 2 thành phần P và D mất tác dụng, thành phần điều khiển mới sẽ “cộng dồn” sai số theo thời gian và làm tăng lực F theo thời gian. Đến một lúc nào đó, lực F đủ lớn để thắng ma sát tĩnh và đẩy xe tiến tiếp về điểm O. Thành phần “cộng dồn” này chính là thành phần I (Integral – tích phân) trong bộ điều khiển PID. Vì chúng ta điều biết, tích phân một đại lượng theo thời gian chính là tổng của đại lượng đó theo thời gian. Bộ điều khiển đến thời điểm này đã đầy đủ là PID:

F=Kp*e+Kd*(de/dt)+Ki*§edt (3)
(dấu § được tôi dùng thay cho dấu tích phân, §edt là tích phân của biến e theo t)

Như vậy, chức năng của từng thành phần trong bộ điều khiển PID giờ đã rõ. Tùy vào mục đích và đối tượng điều khiển mà bộ điều khiển PID có thể được lượt bớt để trở thành bộ điều khiển P, PI hoặc PD. Công việc chính của người thiết kế bộ điều khiển PID là chọn các hệ số Kp, Kd và Ki sao cho bộ điều khiển hoạt động tốt và ổn định (quá trình này gọi là PID gain tuning). Đây không phải là việc dễ dàng vì nó phụ thuộc vào nhiều yếu tố.

Các ứng dụng của thuật toán điều khiển chính xác PID:

Ngày nay hệ thống điều khiển chính xác PID được sử dụng rộng rãi trong các hệ thống tự động hoá như điều khiển lưu lượng nước, điều khiển hệ thống áp suất lò lơi, điều khiển lò nhiệt…

Ở công ty Cổ phần Tập đoàn Công nghệ IDEA, thuật toán điều khiển PID được sử dụng rộng rãi trong các máy tự động phân loại sản phẩm, máy kiểm tra sản phẩm tự động.

Thông tin liên hệ:

Công ty Cổ phần Tập đoàn Công nghệ IDEA

• Đ/C: Nhà xưởng cao tầng, lô 100 KCX Linh Trung 1, P. Linh Trung, Tp. Thủ Đức.
• SĐT: 0931 477 868
• Email: Sales@ideatechmart.com
  Web: https://ideatechmart.com/